우연히 유튜브를 보다가 “JPEG 이미지는 어떻게 압축되는가 (How are Images Compressed?)” 라는 흥미로운 영상을 접하게 되었습니다. 그 과정에서 생각보다 흥미로운 점이 많아서 별도 글로 정리해 보았습니다.
들어가기 전에
간상세포와 원추세포
갑자기 왜 생물학 시간이냐면… JPEG의 압축의 기본 전제로서 중요한 근거로서 작용하고 있기 때문입니다.
간상세포는 명암을 구별하고, 원추세포는 색(파장)을 구별하는 역할을 한다. 사람은 간상세포 수가 월등하게 많기 때문에, 명암에 훨씬 민감하게 반응합니다.
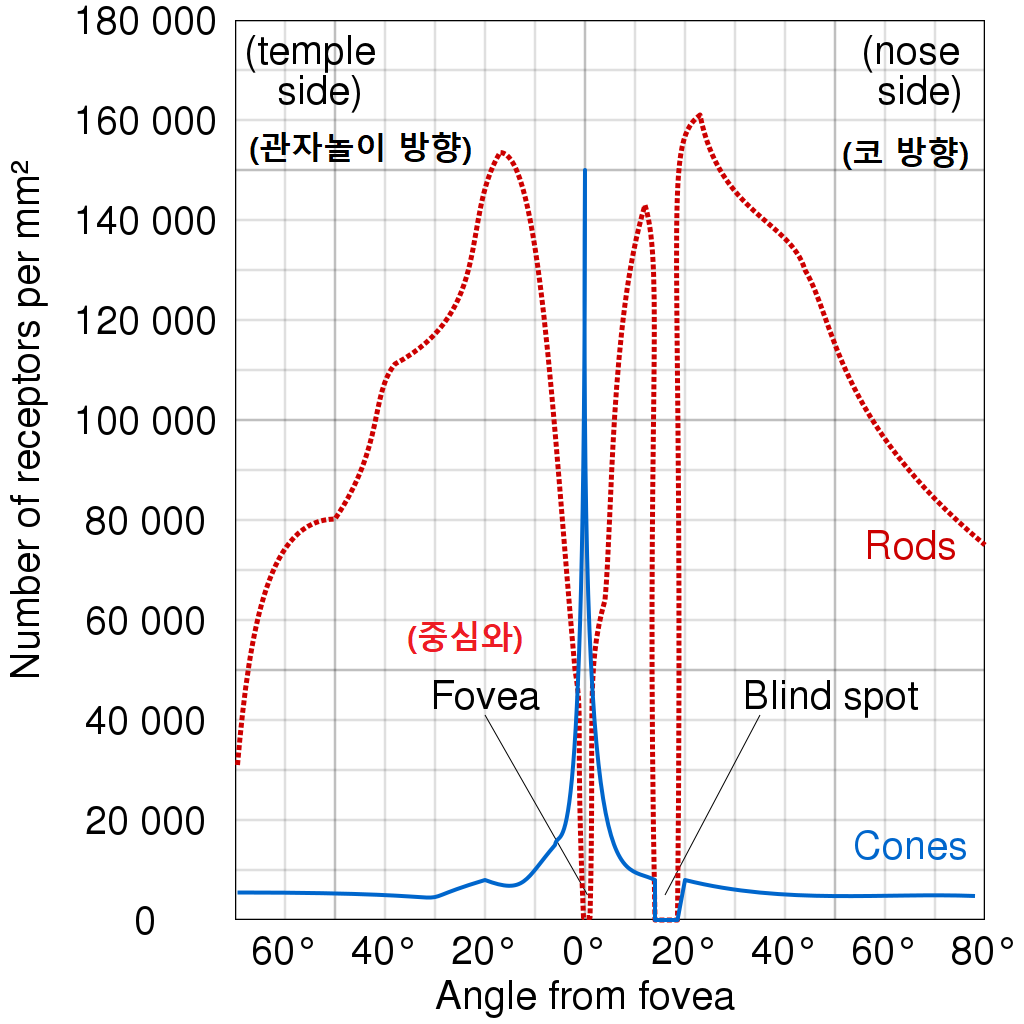
위 사진을 보시면 Rods의 숫자가 Cones보다 월등하게 높은 것을 확인할 수 있습니다.
풍경 사진의 특징
잘 생각해 보면, 풍경 사진에는 압축하기 쉬운 특성이 있는데, 바로 유사한 픽셀을 가진 부분이 꽤 많다는 점입니다. 아래 예시를 보면, 전경과 달리 배경은 단순한 형태임을 알 수 있습니다. 이 특성을 십분 잘 활용하여, 해당 부분을 보다 단순하게 표현하여 저장할 수 있습니다.

JPEG의 전체 알고리즘

- 색상 공간 변환
- 색상정보 (Chrominance) 다운샘플링
- Discrete Cosine 변환
- 양자화
- 허프만 인코딩 수행
실질적인 압축과정은 2부터 시작이고, 2/3/4번 과정은 손실을 동반한 압축입니다. 그렇다면 어떤 부분에서 손실이 일어나는지가 관건이 될 텐데요.

먼저 (1)에서 명암과 색 정보를 분리하여 위와 같이 명암과 색채 정보를 별도로 분리합니다. 그리고 (2) 명암 이외의 레이어(색채)의 해상도를 낮춥니다(=Downsampling). 이는 위에서 이야기한 “사람은 색채 정보에 훨씬 덜 민감하다”라는 사실을 바탕으로 합니다.

이후에 (3)에서는 특정 이미지 구역에 대해서 미리 정해진 패턴을 기반으로 코사인 유사도를 측정합니다. 특정 패턴과 유사도가 높을수록 높은 값을 가지게 됩니다. 이 과정에서 미리 정해진 패턴과 형태가 다른 이미지일수록 손실률이 커지게 됩니다.
동적인 형태가 아닌, 미리 고정된 패턴을 정해놓고 이를 조합하여 이미지를 압축/재생성해내는 기법은 굉장히 신박하다고 생각했습니다.

다음 (4)에서는 양자화를 수행하는데, 여기에서 중요하지 않은(= 사람이 잘 인지하지 못하는) 패턴들은 높은 단위로 양자화시켜서 뭉개버리게 됩니다.
해당 양자화 상수값을 보면 우하단으로 갈 수록 값이 크고, 우하단 패턴들은 대부분 0으로 표시되는 경우가 많음을 알 수 있습니다. 여기서 핵심은 0으로 된 값을 많이 만드는 것입니다.

마지막 (5)에서는 허프만 인코딩을 수행하여 정보를 압축합니다. 해당 과정이 효과가 큰 이유는 바로 앞서 수행한 양자화 때문에 0을 한번에 묶어서 압축할 수 있기 때문입니다. 사실상 기능 측면에서는 (4)와 (5)는 하나의 단계로 묶어도 무방할 것 같습니다.
한가지 재미있는 점은 허프만 인코딩을 대각선 방향으로 iterate 한다는 점이네요. 의미있는 양자화 값 순서대로 돌다 보니 자연스럽게 저렇게 된 거긴 하겠지만요.
단점: Vector image
예로부터 jpg는 벡터 이미지를 저장하기 나쁘다고 잘 알려져 있습니다. 정확히는 선, 원 등의 도형으로 된 사진을 저장하기에 손실률이 크다는 이야기입니다. 그런데 왜 그랬을까요? 구체적으로 어떤 손실이 일어나는 걸까요? 위의 Cosine Transform을 보고 나니 알 수가 있었습니다.

(3)번째 과정의 지정된 테이블에 맞춰서 저장을 해야 하다 보니 저렇게 수직/수평 방향이 아닌 경우 강제로 수직/수평으로 왜곡하게 되어 손실이 일어나게 됩니다. 테이블이 간단해질수록 그 손실률은 더 커질 것이고. 물론 양자화 테이블 자체를 개선하면 더 나아질 수도 있겠지만, 여전히 양자화 이외의 형태가 들어오면 디테일에서 아주 큰 손실을 볼 것임은 자명합니다.
참고로 해당 알고리즘이 동영상에 쓰인 것이 H.264 코덱입니다. (물론 동영상은 그 특성상 delta 처리 관련 인코딩/디코딩 알고리즘도 매우 복잡하다. 별도로 알아봐야 함)
Leetcode 못지 않게, 이미지 프로세싱이나 압축 알고리즘은 그 안을 들여다보면 참 재미있는 것이 많은 것 같습니다. 나중에 시간 나면 PNG나 WEBP도 한번 알아보면 좋을 듯.