구간합 쿼리 문제는 풀 수 있는 방법이 굉장히 다양하다. 그리고 사골 문제 중 하나이다. 그래서 그런지 변형 문제도 꽤 있다. 변형유형까지 다 커버하면 진짜 온갖 종류의 알고리즘 유형들을 다 다루게 된다. 개인적으로 세그먼트 트리가 꽤 재미있는 유형이라고 생각.
Basic: 부분합 w/ K queries
아무튼 문제는 아래와 같다.
1. 배열을 주고,
2. l ~ r 까지의 부분합을 구한다.
3. (2)의 과정을 K번 반복한다.1. Naive
매 요청마다 가능한 모든 경우의 부분합을 구해볼 수 있다.
2중 for loop를 돌아야 하므로 (a, b 두 인덱스를 순회하면서 부분값 계산), 매 최대 부분합을 구할 때마다 O(N^2) 이 걸릴 것이다.
이를 K 번 수행해야 하니 O(K*N).
2. Dynamic
이 문제에서는 제일 효율적인 방법이다. sum array을 만들어서 subtract하기.
f(a, b) = sum(b) - sum(a) 로 구한다. Dynamic으로 느껴지지 않을만큼 미친듯이 간단한 정답이라 뭐 말할것도 없고 ㅋㅋ… Time complexity O(1 * K) 에 Space complexity도 O(n) 이라 준수.
- TMI: 이런 sum 방식으로 결과를 저장해 두었다가 구하는 방법 쿼리 문제에서 은근 종종 보이는 유형인 듯?
3. Segment (분할정복)
사실 이 방식은 여기에 쓰기에는 too much이고, 시간 복잡도도 dynamic보다 못하다. 하지만 언제까지나 가능한 경우임을 언급만 해두는 것으로…
이걸 써야만 하는 경우가 있다! 보다 구체적인 설명은 가장 마지막 유형을 참조할 것.
Sabun: 가장 큰 구간합 구하기
딱히 구간이 있는 게 아니고, 그냥 가장 큰 구간합을 구하는 문제이다.
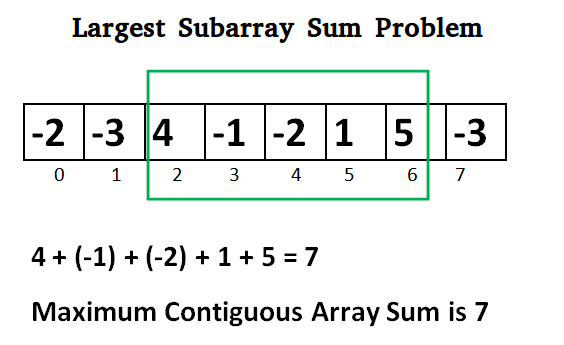
Naive하게는 일일이 모든 구간합을 다 구해보는 것이다. 2중 for loop를 돌아야 하므로 빼박 O(N^2) 확정이다.
optimal한 방법으로는 dynamic이 있다. 0 ~ i 까지의 최대합에 대한 다이나믹을 구하는 것이다.
f(0, i) = max(0, f(0, i-1)) + a[i] 로 점화식을 세울 수 있다. 점화식을 n 번 계산해서 배열을 채운 후, 배열 0~n 까지 한번 돌면 되니 시간 복잡도 무난하게 O(N) .
Time/Space complexity가 O(N^2) 인 방식은 잘못된 방식이다! 굳이 그렇게 짤 필요 없음.
Sabun: K-th로 큰 구간합 구하기
바로 optimal solution을 이야기자면 K 크기의 heap sort를 하면 된다. 물론 모든 경우의 구간합을 찾아야 하므로 기본적으로 time complexity에 O(n^2) 이 들어간다. 그리고 구간합 heaptree를 갱신할때마다 O(k) 이므로, 총 O(kn^2) 의 시간 복잡도.
단골맛집 GeeksforGeeks에도 있다.
Sabun: K 값이 되는 구간합 구하기
알면 쉬운 편인 문제. Two pointer(sliding window)로 풀 수 있다. l, r, sum 변수를 가지고서, sum < K 이면 r을 늘리고, sum > K 이면 l 을 늘리는 방식으로 탐색.
다만 이 문제는 모든 수가 양수여야 한다는 전제사항이 있다. 0~i 까지의 합이 단조증가하는 배열이어야 슬라이딩 윈도우의 왼쪽/오른쪽을 움직일 때 감소/증가가 확정되기 때문.
Sabun: K개의 구간합 구하기 — 하지만 값 수정을 곁들인
세그먼트 트리의 단골 문제중 하나이다. 하지만 면접에는 자주 나오지 않는듯 한데, 아마 세그먼트 트리 자체가 꽤 복잡한 구조인데다가 의외로 현업서 쓰는 곳이 그렇게 많지는 않아서 (?) 한정된 시간 안에 자질을 파악해야하는 인터뷰용 질문으로는 다소 어려워서 그런게 아닐까 싶다. 물론 더 수준높은 곳에서는 볼지도..?
아무튼, 문제가 조금 변형되어서 아래와 같아진다.
1. 배열을 준다.
2. K개의 명령을 수행한다.
2-1. 수정 명령: a 번째 배열의 값을 b로 변경
2-2. 부분합 명령: a 부터 b 까지의 배열의 합 구하기기존 문제에서는 sum 방식으로 구했지만, 이번에는 수정 명령이 들어가서, 이 경우 수정하는데 O(N) 이 소요되게 된다. 이렇게 되면 O(KN) 인 모든 부분합 구하는 방식과 차이가 없어진다…
이 때 segment tree를 이용할 수 있다!
- 수정:
O(log N) - 부분합:
O(log N)
total O(K log N) 으로 준수한 성능을 보여준다.
그렇다면 세그먼트 트리를 어떻게 설계할 수 있을까? 사실 데이터 구조는 힙이랑 똑같다. 다만… 세그먼트 트리의 경우 뭔가 많이 들어간다…

이미지 출처: https://hongjuzzang.github.io/datastructure/segment_tree/
보면 세그먼트 트리의 노드는 (left, right) 값을 따로 내포하고 있는 모습을 볼 수 있다. 따라서, 세그먼트 트리를 탐색하러 갈 땐 heap traversal에서 left / right 값을 추가로 주어야 한다. 그리고 heap과는 달리 상태가 더 복잡하기 때문에(seg left/right 값을 추가로 주거나, 노드 상태에 저장해놓아야 함), 들고 있어야 하는 / 넘겨주어야 하는 상태가 훨씬 많아진다! 그래서 처음에 검색 시그니처 짜고 이해하는 것이 꽤 곤욕이다.
이를테면, 위 그림의 SegmentTree 에서 (2, 5) 의 합을 구하는 것을 나타내면 아래와 같다.
// f: (배열, vector_index, pair<left, right> seg, pair<left, right> query)
// root
f(arr, 1, (2, 5), (0, 7)) = f(arr, 2, (2, 3), (0, 3)) + f(arr, 3, (4, 7), (4, 5))
// second level
f(arr, 2, (2, 3), (0, 3)) = f(arr, 5, (2, 3), (2, 3))
f(arr, 3, (4, 7), (4, 5)) = f(arr, 6, (4, 5), (4, 5))
// 보면 query과 segment range가 완전히 overlapped 되므로, 바로 해당 노드의 값을 리턴하면 됨.보다시피 자료구조가 꽤 복잡하다. 그리고 heap 만들때 1부터 시작하는 vector index도 잊으면 안 된다.
업데이트와 쿼리를 동시에 효율적으로 수행할 수 있다는 특성으로 인해, 요소의 부분 수정을 하면서 동시에 캐시(부분 최소/최대)처럼 사용해야 할 때 종종 사용되는 구조인 듯. DB에서 자주 보는 내부구조 같기도 하고?
하지만 어째 현업에서는 이런 구조로는 잘 안쓰고
TMI1: 백준에 관련 문제가 있다. 2042
TMI2: 세그먼트 트리랑 다른 문제가 얽혀 들어가는 경우가 있는데, 보통 그러면 지옥도가 펼쳐진다. 대표적인 문제가 바로 “최소 공통 조상 찾기(LCA)"의 Optimal solution이다. DFS 탐색을 세그먼트 트리로 빠르게 수행해버리는 즉 동시에 활용하는 (혹은 DP+이진검색) 대표적인 문제이다. 여기 참고.
'개발 > Algorithm' 카테고리의 다른 글
| 몇 가지 Greedy (0) | 2022.07.29 |
|---|---|
| 최소 공통 조상 구하기 (LCA) (0) | 2022.07.28 |
| Peak 찾는 문제 (0) | 2022.07.28 |
| Two-Sum 문제 (0) | 2022.07.28 |
| MST 문제, 그리고 우선순위 큐 (0) | 2022.07.27 |