세그먼트 트리와 더불어 기본적인 알고리즘 유형 중에서 꽤 어려운 편이라고 생각하는 유형 중 하나이다.
사실 이미 잘 설명해 놓은 사이트들이 많지만, 굳이 포스트를 또 쓰는 이유는 설명이 그냥 내 마음에 안 들어서 (…)
문제는 아래와 같다.
어떤 트리가 있고, 그 트리에서 두 노드를 골랐을 때, 그 두 노드의 가장 가까운 공통조상을 찾으세요풀이
Naive 방법은, 그냥 각 노드의 부모를 타고 계속 올라가면서 비교하는 것이다. 여기서 조금 더 최적화를 하자면, height를 맞춰서 부모를 계속 타고 올라가는 것이다.
Optimal하게 푸는 방법은 2가지가 있다.
1. DP + 이진 탐색
위에서 쓴 Naive 솔루션에서, 이진 탐색을 통해 보다 빠르게 공통조상을 찾는 과정이 추가되어 있다. 이게 가능한 이유는, 어떤 숫자든지 sigma(k=1; k<n; ++k) k_n*2^n 꼴로 표현 가능하고(이거 좀 더 엘레강트하게 표현할 수 있는게 뭐였는지 까먹…), 따라서 저 조합만큼의 부모조상 테스트를 해보면 찾을 수 있다. 이를테면…
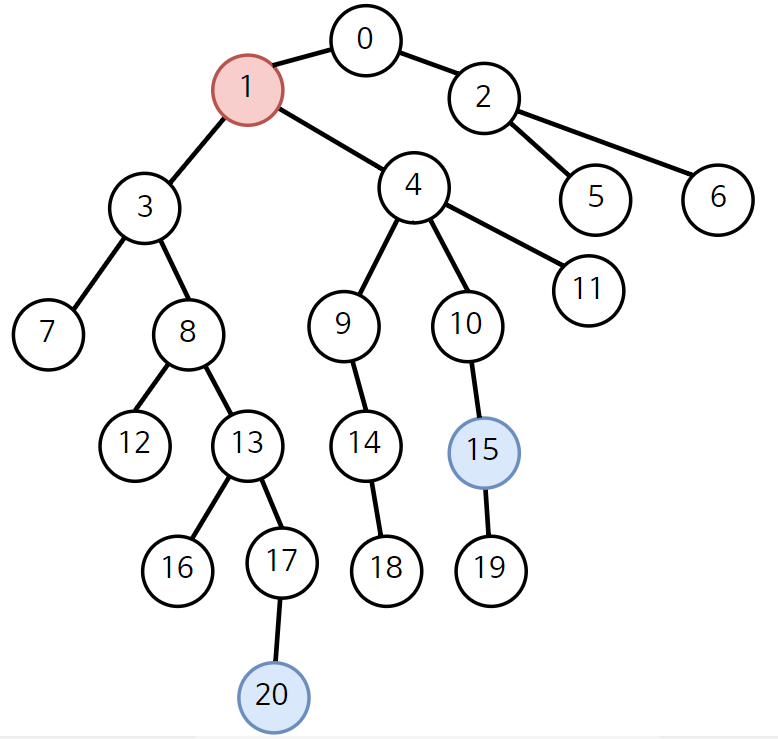
위 그림에서 20=>13, 15 노드 두개를 검사한다고 했을 때
4번째 공통조상: 각각 (0, 0) => 동일하긴 한데 최소 공통조상이 아니라 pass
2번째 공통조상: 각각 (4, 3) => 동일하지 않지만 keep
(현재 노드를 (13,15) => (4,3) 으로 수정)
1번째 공통조상: (1, 1) => 정답 찾음.
즉, 3번째 조상인 (1) 노드가 LCA 이다.
공통조상 검색을 4개의 조상 모두를 확인하지 않고, 3번만 확인해서 찾을 수 있었음.따라서 결론적으로 모든 부모조상을 안 살펴보고 공통조상을 찾을 수 있다 (= 이진탐색). 또 보통 해당 문제는 M개의 쿼리가 주어지는 형태로 오기 때문에, 부모조상을 cache 하게 된다. ⇒ DP 테이블로 만들어 씀.
이 부분은 친절하게 쓴 다른 블로그들이 많이 있으니 그걸 읽는게 좋을 듯.
시간복잡도는 DP 테이블 생성에 O(NlogN) , 이진검색에 O(logN) 을 소요. M개 쿼리가 들어오면 O(MlogN) .
2. DFS + 세그먼트 트리
사실 이거 이해하는게 나한테 좀 당혹스러웠다. 알고 보면 별거 없는데…
원리는 이것이다: Node A부터 Node B까지 DFS로 순회한 내역을 알면 최소 공통 조상을 찾을 수 있다
아래 예시를 보면,
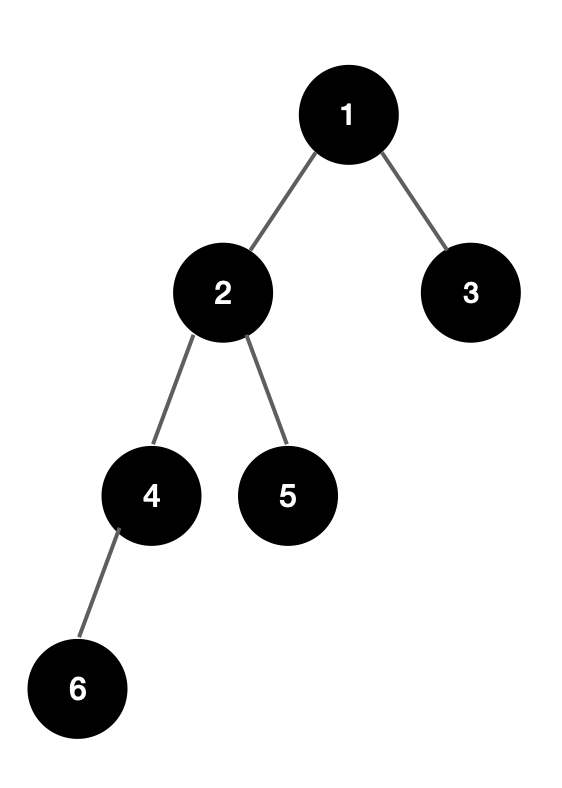
여기에서 6과 5의 공통조상을 찾는다고 가정해보자.
- 일단 전체 DFS(root > left > right) 순서를 보면 아래와 같다:
[1 2 4 6 4 2 5 2 1 3] - 여기에서 6 to 5를 보면 아래와 같다:
[6 4 2 5] - 그럼 여기에서 최소 공통 조상은 minimum ⇒ “2” 임이 자명하네!
이거 은근히 신기하다 ㅋㅋ 한번도 생각해 본 적 없는 내용이라 그런가…
무튼, 이걸 매번 DFS 만들어서 쿼리하는 것은 상당한 비용(O(MNlogN)) 을 요구하기 때문에, 이 쿼리 자체를 세그먼트 트리로 해버리면 훨씬 효율적으로 할 수 있다는 것이 이 문제의 핵심 키포인트다.
DFS 쿼리를 만들기 위해서, DFS 선 순회 하고 “N번째 노드가 처음 방문되는 trip의 시점"을 저장해놓는 배열만 만들면 된다. 이 작업들은 시간복잡도 O(N).
총 시간복잡도 상 큰 차이는 없지만(O(MlogN)), 세그먼트 트리가 더 빠르다는 이야기가 있다. DP의 경우 테이블 생성에 다소 비용이 드는 이유에서이다. 정확한 이유는 잘 모르겠다. 공부가 더 필요함. 여기 참조.
이미지 출처
'개발 > Algorithm' 카테고리의 다른 글
| 자주 나오는 대회용 알고리즘 정리 (0) | 2022.08.30 |
|---|---|
| 몇 가지 Greedy (0) | 2022.07.29 |
| K개의 구간합 구하기 (0) | 2022.07.28 |
| Peak 찾는 문제 (0) | 2022.07.28 |
| Two-Sum 문제 (0) | 2022.07.28 |