22/10/08 변경사항: 이제 고급 알고리즘이라고 보기에는 대부분의 내용이 부합하지 않기에, 제목을 변경했습니다.
스스로 복습해볼 겸 하여, 경시문제에서 나오는 알고리즘 패턴들을 몇가지 정리해 두었습니다. 당연히 실무에서 쓰일 일은 거의 없겠으나, 솔루션을 도출하기까지 사용하는 자료구조나 사고과정에 대해서는 꽤 흥미로운 것이 많다고 생각합니다.
분할 정복 관련
분할 정복의 가장 대표적인 예라면 Merge sort가 있을 것입니다. 문제를 자그마한 단계로 나누어서 해결하는 방법인데, 의외로 두 수의 곱 문제를 해당 방식으로 푸는 기법이 있더라고요.
두 수의 곱
큰 두 수의 곱을 수행하는 건 쉬운일이 아닙니다. 컴퓨터한테도 마찬가지인데, 이를 분할 정복으로 풀 수 있다고 합니다.
1. FFT (Fast Fourier Transformation)
이 문제를 FFT로 풀 거라고는 생각도 못 했고, FFT가 분할 정복일 거라는 생각 또한 해본적 없는데, 굉장히 의외였습니다. 알고리즘도 FFT로 풀어야 하는 세상이 왔다는 게 허허… 😨
재미있는 점은,
- 일단 이 문제를 FFT로 풀면, x=10 으로 분리하여 계산을 해야 합니다. (당연하지만)
- 기본적으로 Naive solution은 모든 컨볼루션을 구해야 하기 때문에
O(n^2)이 걸린다는 것도 알아둘 필요가 있음. (기본 수학도 잘 안 쓰면 기억이 안 난다…) - 핵심은 쿨리-튜키 알고리즘입니다. 허수 어쩌고 있는데, 너무 복잡하게 생각할 것 없이 계수를
O(nlogn)에 구하기 위해서 임시로 치환하는 거라고 생각하면 편함.- 하나 또 놓치면 안 되는게, 허수의 초기값은 cos(2PI/n), sin(2PI/n) 이 자명합니다. 최대 n 항만큼의 다른 값을 만들어야 하니까 그렇겠지..?
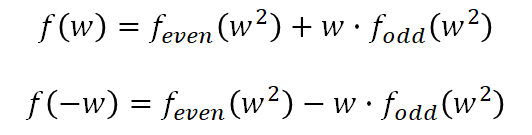
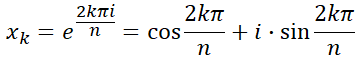
- conquer 쪽이 좀 어려울 수 있는데, 그냥
f(w) + f(-w) + f(w^2) + f(-w^2) + ... + f(-w^((n-1)/2)) == f(w) + f(w^2) + ... + f(w^(n-1))입니다. 즉 DFT 계산을 한 겁니다! (DFT 정의가 이렇습니다!) 이게 어떻게 되냐고 묻는다면, 허수의 180도는 반대 방향이기 때문이고, 360도(=2n)은 원래 값과 같기 때문입니다. 진짜 겁나 어렵다… - 그렇게 FFT를 수행하고, 두 DFT(값)를 곱한 후, 이에 대해 IDFT를 수행하면 두 항의 곱을 알 수 있다고 합니다. IDFT는 DFT의 반대 과정이기 때문에, FFT를 한번 더 수행하고 있는 것을 볼 수 있습니다. 신기한 건 DFT를 벡터 곱하듯 마냥 곱해버리네? 😅 IDFT 쪽은 그냥 그런갑다 합시다. 저도 잘 모릅니다.
- 의외로 C++에서 허수(a + bi)를 표현할 수 있는 템플릿이 이미 있더라고요?
std::complex, 자주 쓸 일은 없겠지만 하나 알아갑니다. - 물론 실제 세상에서의 FFT(특히 음원에서 쓰는 것) 접근 방법이랑은 비슷한 듯 조금 다릅니다. 기본적인 접근 방식과도 다르고, 샘플링 사이즈도 있고 클리핑 등 추가적인 변수들이 더 있음… 이건 이후에 별도 포스트로 다룰 수 있으면 좋겠네요.
https://m.blog.naver.com/kks227/221633584963
https://www.acmicpc.net/problem/13277
2. 카라츠바 곱셈
위의 머리 터지는 FFT에 비하면 간단한 편이긴 합니다. 일종의 수학적 꼼수긴 한데, 핵심은 a * b를 (a1 + b0) * (b1 + b0) 꼴로 만들었을 때 이를 네번이 아니라 세번의 곱셈으로만 계산할 수 있다는 데 있습니다.
사실 수학적 꼼수(?)라서 아래 식을 외워서 구하면 됩니다.
z2 = a1 * b1;
z0 = a0 * b0;
z1 = (a0 + a1) * (b0 + b1) - z0 - z2;시간 복잡도는 O(n^log3).
https://velog.io/@qwe910205/카라츠바의-빠른-곱셈-알고리즘
탐색 관련 유형
보통 탐색 관련 유형은 높은 확률로 이진탐색을 쓰는데, 정렬된 데이터가 있으면 십중팔구 이진탐색입니다. 단조 증가/감소의 경우 모든 값을 탐색할 필요가 없다는 것이 모티브이기 때문이니까요.
혹은, 정렬이 안 되어 있어도 naive가 O(nlogn) 이상이라면, 정렬+이진탐색 전략을 고려해 볼만 합니다.
솔직히 대회용 알고리즘이라 써놓고, 그래프에 어지간한 유형은 다 긁어다가 놨습니다 😅 개인적으로 그래프 알고리즘의 기본적인 난이도를 높게 보는 게 반영된 것 같습니다.
이 분야는 워낙 variation이 많아서 독립적으로 이진 탐색만 쓰이는 경우는 거의 없습니다만 (보통 다른 알고리즘들과 섞여쓰여 난이도를 지옥으로 만듬), 나중에 생각나면 정리해 보는걸로…
삼분 탐색
이진 탐색이 단순 함수가 단조 증가/감소 할 때만 쓸 수 있었다면, 삼분 탐색은 함수가 위로 볼록/아래로 볼록(극댓값, 극솟값)을 가진 경우에 쓸만합니다. 은근히 쓸데가 있을 법한 기법이라서 고급이라고 하기에는 꽤 알아두면 좋을 문제 해결 방법.
https://m.blog.naver.com/kks227/221432986308
- 근데 생각해보면 요즘 ML같은데서 써먹을 좋은 그라디언트 메서드 많아서 그닥 안 유용할지도… 🤔
그래프 및 유량 관련
많이 쓰이는 기본적인 알고리즘 (DST/BST, Prim, Kruskal, 백트래킹 등)에 대해서는 미리 머리속에 담아두는 것이 좋습니다. 덤으로 최대 유량 문제에서는 정석으로 알려져있는 포드-폴커슨 알고리즘까지는 기본으로 들고가는 것이 이 부분 소양.
다만 실무에서는 제일 마주칠 일이 없는 알고리즘 부류 중 하나라고 봅니다. 그래도 sparse/dense 그래프에 대한 접근법에 대한 기본 소양은 알고 있으면 좋음.
서큘레이션 문제
그래프의 특정 노드들에 대해 in/out 최대값을 지정했을 때, 해당 조건을 만족하는 흐름이 있는지를 확인하는 문제입니다.
문제 조건이 많아서 꽤 복잡한데, 다행히 이 문제도 포드 마냥 본래의 그래프를 변형하여 풀 수 있습니다. 아래처럼 in/out 노드들 각각에 대한 종점 노드를 새로 만들어서, 이에 대한 최대 유량을 체크하는 방식으로 풀 수 있습니다. 분명 흐름이 없는 서큘레이션 그래프였는데, 아주 무난한 흐름이 있는 그래프로 변환된 것을 확인할 수 있습니다.

(출처: 아래 주소의 Ries님 블로그)
하나 또 변형 유형은, 간선의 하한이 있는 경우입니다. 이 때는 하한이 있는 엣지의 시작 노드에 가중치를 주는 방식으로 문제를 변환할 수 있다고 합니다. 즉 동일 유형으로 풀 수 있는 것입니다.
이건 모르면 얻어맞는(?) 문제입니다. 특히 그래프쪽이 유독 이게 좀 심한 것 같습니다. 별로 문제로 써먹기에 내키지 않는 이유 …
https://m.blog.naver.com/kks227/221426339344
최단경로 알고리즘
너무나… 유명한 알고리즘이 3개가 있습니다. 각각마다 특성이 다 다르니, 언제 어느것을 이용해야 하는지만 간단하게 훑는 정도로만 다루고 넘어감.
워낙 유명한데 정작 실무에서 쓸 일이 없어서 (…) 순전 대회용이라고 (개인적으로는) 생각합니다.
- 다익스트라: 정점에 대해서 값을 갱신하고, 갱신된 값은 사용하지 않음. 방문해야 하는 노드의 순서를 정하는 것이 꽤 핵심이라는 것을 잊으면 안 되는데, 이를 위해 heapsort(priority queue) 이용하는 것이 의외의 핵심!
O(ElogV) - 벨만-포드: 간선 위주로 값을 갱신합니다. 음의 간선에 대해서 사용할 수 있고, 음의 사이클 여부 물어보는 문제 나오면 십중팔구 이 문제. 시간 복잡도와 음의 사이클에 대해서 알고 있어야 하는 게 포인트라고 봄.
O(VE) - 플로이드-와샬: 접근 방법은 벨만포드와 비슷하지만 DP 특유의 깔끔한(?) 코드가 꽤 인상깊기 때문에 한번쯤 손으로 구현해 볼 필요가 있다고 생각함. 사실상 벨만포드 상위호환 느낌.
O(V^3)
꼬은(?) 유형 중 엄청 유명한 것 중 하나가 축사 배정이 있으니, 이건 한번 봐 두면 좋을 듯. 미리 쓰자면, 처음 노드와 끝 노드로 묶는 패턴은 굉장히 많이 쓰이는 편입니다.
정점을 한번(N번)만 지나는 변형 패턴도 알아두면 좋습니다.

사진 출처: https://m.blog.naver.com/kks227/220804885235
위상정렬
이건 대회용이라고 하기에는 너무 흔한 알고리즘이지만… 이상하게 가끔씩 존재감이 잊혀지는 느낌이 있어 자리 한 칸 주었습니다.
Cycle을 구하거나(사실 이건 DAG로도 되어서 그닥 중요 X), 선행순서를 잘 맞춰서 순서를 정리한다거나~ 할 때 필수적으로 쓰게 됩니다. Queue와 inbound를 사용하는 것이 핵심이라는 것을 잊지만 않으면 될 듯.
개인적으로는 은근히 흔히 쓰이는 구현이라고 생각합니다. 머리속에 상시저장공간 할당해 줄 가치가 있음.
https://m.blog.naver.com/kks227/220800013823
최대 유량 알고리즘: 디닉 알고리즘
유량 알고리즘도 종류가 여러가지가 있습니다.
- 포드-폴커슨: 널리 알려져있고 간단한 편, 시간 복잡도가 최대유량에 비례하는 특징이 있어 한계가 있음!!
O((E+V)*F) - 애드몬드-카프: 시간복잡도
O(V * E^2), sparse한 그래프에서 효율이 좋다- 아주 간단히만 쓰면, 포드-폴커슨의 BFS 버전.
- 가장 대중적인 픽
- 디닉 알고리즘: 시간복잡도
O(V^2 * E), dense한 그래프에서 효율이 좋다
솔직히 애드몬드 정도면 충분하다고 보는데, 가끔 디닉을 쓸 수밖에 없도록 강요하는 문제가 나오게 됩니다. 😨
디닉 알고리즘의 포인트는 “레벨"입니다. 일종의 BFS와 비슷한 느낌이라는 생각인데, 여기서 iteration을 반복할 때 닫힌 노드에 대해서는 그래프에서 제외하는 게 알고리즘의 핵심입니다. 유량 구하는 것 자체는 대충 dfs로 V^2 루프 돌면서 구합니다. 백프로파게이션 없어서 포드폴커슨같이 추가 복잡도는 없습니다. 전반적으로, 생각보다 알고리즘 자체는 간단합니다.
무지막지하게 큰 그래프 주고서 굳이 유량 구하겠다고 이렇게까지 시간복잡도를 고려해가며 알고리즘을 써야 되는 이런 케이스가 진짜 경시대회 문제 최적화긴 하죠 (…)
https://m.blog.naver.com/kks227/220812858041
TMI: 이분 매칭 (호프크로프트 카프 알고리즘)
… 정도면 끝일 줄 알았는데 하나 더 남아 있네요 😨 근데 이 알고리즘은 이분 매칭에서만 쓰이는 특수한 케이스라고 합니다.
디닉과 연관이 있는 게, 여기도 레벨 매칭을 합니다. 매칭에 속하지 않은 정점을 레벨 0이라고 가정하여 알고리즘을 수행하는 방식이라고 하네요. 필요하다면 기존 결정된 노드를 선점할 수도 있습니다 (이 부분은 일반 이분 매칭과 동일).
거의 쓰일 일은 없을 것 같지만 이분매칭이라면 한 번쯤 곱씹어볼만한 문제이기 때문에 적어만 둡니다.
https://m.blog.naver.com/kks227/220816033373
최소 컷 문제
최소한의 비용으로 두 정점을 분리하라는 문제입니다. 그런데 한가지 알아야 되는 사실은 두 정점을 분리하는 비용은 두 정점간의 최대유량과 일치한다는 것입니다. 따라서 최대유량과 동일한 문제가 되게 됩니다. 최대유량을 구했을 때, 해당 최대유량과 일치하는 용량을 가진 edge 우선으로 선택하면 최소컷이 됩니다.

https://m.blog.naver.com/kks227/220808685331
2-SAT (+ SCC)
학부 알고리즘 시간에 분명 배운 적이 있는 내용인데, 그땐 “도대체 이런 거 배워서 뭣한담"하면서 투덜거렸던 기억이 있습니다… 그리고 지금 이렇게 저를 다시 찾아왔네요 😨
먼저 “SAT 문제”에 대한 정의부터 다시 짚고 넘어가면, 여러개의 bool 변수들로 이루어진 식을 어떻게든 true로 만들 수 있는지에 대한 문제입니다. 그리고 2-SAT는 각 절에 들어가 잇는 변수가 2개인 것을 의미합니다. (A v B) ^ (C v D) 같은 식에서, (A v B) 가 절에 해당하는 개념입니다. (참고로 3-SAT는 NP-Hard로 알려져 있음)
재미있는 것은 해당 문제가 그래프 문제로 치환된다는 점입니다. 그리고 이를 위해 SAT 절을 명제로 치환하는 과정을 필요로 합니다. 예시를 하나 들면, (A v B) 는 !A => B, !B => A 가 필요조건에 대한 명제가 됩니다. 이렇게 끌어낸 명제들을 가지고 X_a ⇒ !X_a 꼴로 가는 그래프를 만들 수 있습니다. 그리고 해당 그래프에서 SCC(Strongly connected component; 어떠한 정점에도 도달 가능한 연결 형태)를 찾는 것이 핵심입니다. 왜냐면 SCC 안의 명제 중에 참/거짓을 동시에 만족해야 하는 (e.g. X1 ⇒ !X1) 꼴의 명제가 있다면, 해당 명제는 참이 될 수 없다는 것을 알 수 있기 때문입니다.
이러한 경우가 없다면, 식을 반드시 참으로 만들 수 있는 경우가 있다는 사실은 자명하다고 합니다.
SCC를 구하는 방법에 대해서는 간단히만 언급하면 DFSN + Stack 사용해서 component를 구할 수 있습니다. Push 하는 조건은 descendant로 갈 때, Pop하는 조건은 더 이상 ancestor로 갈 수 없을 때.
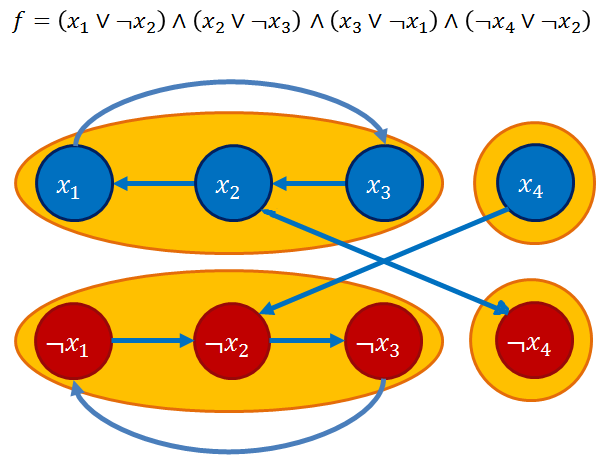
문제가 명시적으로 2-SAT이라는 것을 말해주지 않는 경우가 많아서 이를 파악하는 게 첫번째 관문입니다. 얼핏 보면 이분매칭이랑 헷갈리기도 하고… 파생 유형들을 풀어봅시다.
https://m.blog.naver.com/kks227/220803009418
BCC
SCC를 마찬가지로 학부 알고리즘때 봤었고 어디 쓰나 싶었던 알고리즘인데 … 비슷한 BCC를 간단히 적어놓습니다. 물론 지금 봐도 어디 쓰나… 싶은 생각은 들지만 🤔
정의 자체는 SCC와 비슷한데, “컴포넌트 안의 속한 정점 하나를 지워도 서로의 정점에 도달할 수 있는 경우가 존재"입니다. 다만 이 경우는 무향 그래프(bi-directional)에 보다 부합하는 조건이 됩니다.
핵심은 DFSN + 역방향 간선 찾기입니다. 이를 위해서 간선을 넣는 스택 자료구조를 사용하고요. 이걸 이용해서 BCC 컴포넌트를 구성할 수 있습니다.
하나 또 헷갈릴 수 있는게, 하나의 간선과 두 정점도 BCC입니다. 정의를 제대로 짚고 넘어가야 알고리즘을 제대로 간파할 수 있습니다. 직관적인 요구사항에 비해 구현에서는 세부사항을 잘 알아야 하는 점이 있어서 재미있는 문제라고 생각함.
블록-컷-트리
(사실 이건 트리 관련 유형이지만) 이를 이용해서 cycle이 있는 그래프를 BCC를 포함한 트리로 바꾸는 문제가 있습니다. 이를 바로 블록-컷-트리 문제라고 하는데, BCC를 제대로 이해했다면 간단하게 볼만한 정도라고 생각됩니다. (물론 세부 구현은 스킵)
한 가지 캐치해야 할 것은, BCC와 블록-컷-트리 자료구조는 별개입니다. 따로 구조를 만드는 방식으로 알고리즘이 구현되어 있다는 점입니다.
https://m.blog.naver.com/kks227/221475472155
오일러 경로
오일러 “회로”와 경로의 정의부터 정확하게 짚고 넘어가야 합니다. 경로는 모든 간선을 1번씩 통과하는 경우이고, 회로는 거기에 시작 정점으로 돌아오는 경우.
오일러 회로의 존재여부를 구하는 방법은 널리 알려져 있는데 차수가 홀수인 정점이 2개일 때 경로, 0개면 회로입니다. 방향성이 있는 그래프는 in/out degree가 동일해야 하고.
풀이 자체는 간단한 편인데, 모든 edge를 다 쓸 때까지 계속해서 DFS를 수행하고, “끼워넣기"하면 됩니다.
한가지 유의해야 할 패턴 중 하나는, input 그래프 자체가 여러 컴포넌트로 나뉘어져 있는 경우입니다. 가끔 edge case로 나오는 경우가 있음.
사실 이 자체만으로는 고급 알고리즘이라기에는 조금 흔한 문제 중 하나이나, (그래프 문제는 언제나 그렇듯…) 자꾸 잊어먹기에 다시 한번 recall하는 의미에서 적어놓음.
https://m.blog.naver.com/kks227/220800097205
트리 관련
트리 관련해서도 어려운 문제가 꽤 있는데 그 중 종종 봤었고 인상 깊었던(?) 문제들.
참고로 많은 알고리즘들이 세그먼트 트리를 근간으로 하고 있습니다. 솔직히 이것도 고급축이라고 보지만, 일단 기본 소양으로 알아놓고 봐야 좋습니다.
레이지 프로파게이션
으레 쿼리 문제+세그먼트 트리 문제면 90% 확률로 이 친구라고 봅니다. 여기부터는 실제로 구현하기에는 좀 짜증나는 부분이지만 이 정도까지의 알고리즘은 원리라도 알아둘 필요가 있다고 봅니다. 이 알고리즘은 안 쓸 지언정 Prod에서의 partial update의 소중함이란 말이지…
https://m.blog.naver.com/kks227/220824350353
LCA (최소 공통 조상)
아 이문제 너무 싫어요!!! 😇 문제도 굉장히 복잡하고 풀이도 굉장히 복잡합니다. 그래도 한번쯤은 진득하게 봐두면 나쁘지 않습니다.
의외로 이진검색이 안에 내포되어 있다는 게 문제 이해의 팁입니다.
거지같은
복합 유형의 좋은 예 중 하나. 덕분에 O(N) 대신 O(logN) 으로 시간복잡도를 내릴 수 있는 것입니다.
https://m.blog.naver.com/kks227/220820773477
헤비-라이트 디컴포지션
모티브는 트리를 굵은 그룹에서부터 작은 그룹으로 나누는 작업인데… 코드를 짜는게 너무 tricky해 보여서 알고리즘 문제로서의 가치는 좀 모르겠습니다 🤔 그래도 이런 문제에서 이런 식으로 접근해야 한다~ 라는 것 정도는 알아두면 좋아 보임.
https://m.blog.naver.com/kks227/221413353934
Meet in the middle
아이디어는 단순한데, BFS의 최적화 기법으로 꽤 실제로도 써먹기 좋은 기법이라고 생각합니다. (정작 문제로서는 본 적이 없네요)
https://m.blog.naver.com/kks227/221382873753
DP
간단한 문제는 쉬운데 (예: 피보나치, 간단한 점화식 등), 어려운 문제는 답도 없습니다. 라고 말은 썼지만 저는 DP쪽에 정말 조예가 없어서 잘 모릅니다 (…) 그래도 몇 가지 인상깊었던 유형들 위주로만 정리해 둡니다.
행렬을 이용하는 방식
갑자기 행렬이 왜 나오냐면, 잘 생각해보면 특정 점화식은 행렬의 곱으로 표현이 가능한 경우가 있기 때문입니다.
예를 들면, (F_n, F_n-1) = M * (F_n-1, F_n-2) 꼴 같은 것인데, 여기까지 문제를 추론할 수 있다면 M^n을 구하는 것만으로 F_n을 구할수가 있습니다. 이런 유형 처음 보고서 되게 신박했던 경험이 있네요.
https://m.blog.naver.com/kks227/221383409543
Convex Hull Trick
의외로 도형 문제중에 DP가 있더라고요? CCW나 있는 줄 알았는디…
사실 다이나믹이라고 보기에 좀 애매할 수도 있는데… 개인적으로는 스위핑+이진탐색에 가까운 문제라고 생각되기도 합니다. 역시 단조증가/감소의 특성을 가지기 때문에 가능한 문제풀이입니다. 1차 함수로 표현된다고 하면 거진 그런 꼴의 문제라고 볼 수 있다는 것…
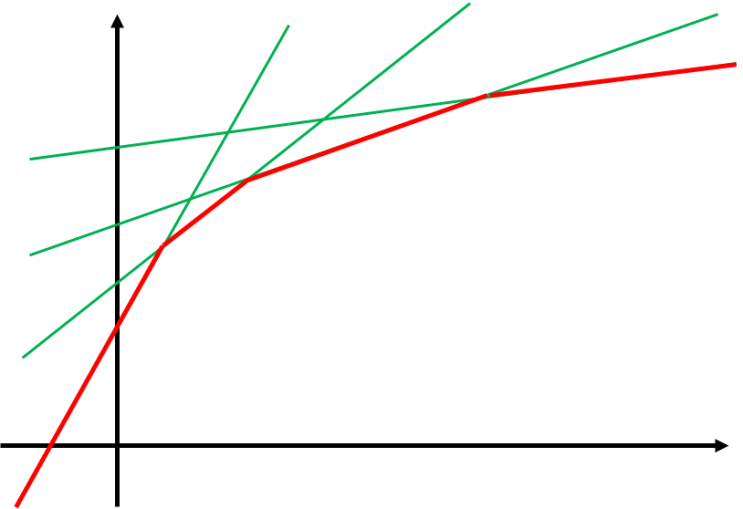
핵심을 담고 있는 이미지는 이것이라고 생각이 되네요. (출처는 아래 링크입니다: Ries님)
https://m.blog.naver.com/kks227/221418495037
의외로 이 알고리즘이 유용하게 쓰이는 곳이 있는데, 바로 MIDI BPM을 계산하는 부분입니다. BPM은 beat와 minute의 상관관계를 나타내는 여러 함수(x: beat, y: time?) 들의 집합이 주어졌을 때에, beat ~ time conversion 하는 경우 유용하게 씁니다.
기타 (?)
개인적으로 DP라기보다는 상태를 잘 저장해야 하는 그리디 느낌이 물씬 풍기는 듯(…)
- 전처리 사용: 0~N 까지의 합을 미리 구해놓고(prefix sum) 풀면 훨씬 쉽게 풀리는 문제들이 있습니다. 최대 부분합 문제가 그러한 예시 중 하나. (DP라고 하기에는 그리디에가까운 느낌이기도 하고…)
- 이외에도 소트 등 전처리가 필요한 경우가 있습니다. (이걸 해야만 DP가 보인다는 게 난이도를 배로 올리는 주범…)
- 모노토닉 큐: 가끔가다 튀어나오는데 얼핏 봐서는 풀기 겁나 까다롭습니다. 값을 넣고 빼는 경우를 잘 고려해야 하는데, 새로 들어온 값보다 더 적은 기존 값들이 있으면 모조리 날려버리고, 새로 들어온 값이 더 작을 경우에는 그대로 저장하면 되는 걸 잘 이해해야 합니다.
- N개의 서브테스크: 여러개의 서브테스크와 이에 대한 복잡한 규칙을 주고서, 이것들을 수행 시 드는 최소 비용을 구하라고 하는 경우가 있습니다. 각 서브테스크별로 다이나믹 테이블을 만들면 비교적 쉽게 모델링 가능합니다. (약간 거스름돈 가짓수 구하는 문제 비슷하게 하는데, 조건이 복잡한 경우라고 보면 됩니다. 모노토닉 큐랑 혼합해서 쓰이는 경우도 있음) — 좋은 예시로는 요리 문제
기타…
string 관련이나 유명한 Greedy 몇 가지.
비트마스킹
알면 정말 별거 없고, 솔직히 실무 0티어 분야가 아닐까 싶습니다 (Low-level 코더일수록 ㅎ). 개인적으로는 그냥 struct 쓸 것을 간단하게 int 타입으로 묶는 그런 느낌이고, 요상하게 DP랑 많이 엮임. 한 가지 주의할 점은 이걸 쓸 일은 거의 없다는 건데, space complexity를 잘 염두에 두어야…
엄연한 하나의 방법이기 때문에 마크만 해 둠.
https://m.blog.naver.com/kks227/220787042377
스위핑 기법
대표적인 문제는 선 긋기 문제입니다. 수평선 위에 그은 선분의 길이 총합을 구하라는 건데 막상 처음 접하면 상당히 골 때려서…
핵심은 input을 정렬한 후, 현재 선분을 합치다가, 못 합치면 새로 긋기 입니다. 아주 잘 정리된 글이 있어 또 링크를 …
https://m.blog.naver.com/kks227/220907708368
겹치지 않고 예매하는 문제
이건 스위핑 기법이라고 봐야 하나 애매하긴 한데 비슷하니까 그냥 안에 집어놓음… 흠…
비행기표, 독서실 등… 수십가지의 바리에이션이 있지만 문제는 다 똑같습니다 😅
어렵지는 않은데, 이상할 정도로 자주 보여서 리스트에만 올려 놓음. 해답은 간단한데, descending order by starting time 하면 됩니다. 가장 큰 start time이 최적의 해이기 때문에 자명한 이야기.
2차원에서의 스위핑
이거 아주 짜증나는데… 경시대회에서는 무슨 국밥마냥 심심하면 나옵니다. tricky한 요소도 많아서 조심해야 하기도 함.
그와중에 재미있는 점은 99%는 세그먼트 트리가 필수적으로 사용된다는 겁니다. 시간 내에 답을 도출하려면 어쩔수가 없는데… 그래도 Naive하게 접근하는 방법이라도 알아두는 것이 좋습니다. 그리고 그 근간은 sort/x, y sweeping 에 있습니다. 아무래도 생각보다 처음 보면 당황하기 좋은 유형이라서.
부분 문자열 찾기 (KMP)
일종의 오토마타 테이블 만들기인데, 이거 볼 때마다 까먹고 (어차피 Regex 쓰니깐) 실제 쓸모는 없고… 그래도 strcmp() 실패할 때마다 매번 다시 검색하는 O(N*M) 같은 헛소리를 하지 않도록 하는 데 있어서의 근거로 알아둘 필요는 있습니다.
https://m.blog.naver.com/kks227/220917078260
이거 말고 아호코라식도 있던데 딱히 보고 싶지는 않네요… 다만 이것도 알아두면 좋은게, *K개의 문자열에 대한 매칭을 동시에 효율적으로 한다는 점.***
또 하나: 라빈카프도 있습니다. 해시테이블 활용도에 있어서 좋은 용례.
중국인의 나머지 정리
유명한 정수론 중 하나입니다. 아주 간단히 설명하면, 서로소인 나머지(mod)들에 대한 연립방정식(연립합동식)은 해가 단 하나 존재한다는 것.
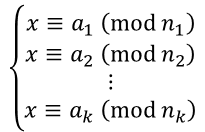
서로소가 아닌 나머지들이 들어올 경우에는 소인수 분리를 해야 합니다. 그리고 저 x를 구하는 방법은 확장 유클리드 알고리즘으로 구할 수 있습니다.
거의 활용도 0에 가깝지만 그냥 정수론은 … 재밌으니까 ㅎ…
https://m.blog.naver.com/kks227/221635322468
써놓고 보니 고급 알고리즘이라는 말이 민망하게 그냥 집대성이네요 ㅠㅠ… 그래도 이 정도는 저같이 연 없는 사람도 자주 봐왔고 좋은 자료구조를 활용하고 있는 문제이니만큼 알아두어 나쁠 것은 없는 문제들이라고 봅니다.
그래도 … 이후에 생각이 난다면 내용을 더 갱신해 두겠습니다.
Part2로 새로 포스트를 써야 할 듯.
PS) 문자열 검색쪽은 마이너한 유형이라고 생각해서 여기서는 일부러 배제해 두었습니다. 이후에 별도로 정리해 볼 예정.
'개발 > Algorithm' 카테고리의 다른 글
| Parser에 대해서 알아보자 (0) | 2022.09.04 |
|---|---|
| Audio Data의 Pitch를 변경해보자 (0) | 2022.08.31 |
| 몇 가지 Greedy (0) | 2022.07.29 |
| 최소 공통 조상 구하기 (LCA) (0) | 2022.07.28 |
| K개의 구간합 구하기 (0) | 2022.07.28 |